Продолжаем знакомиться с возможностями пакета Prophet. Это сообщение содержит описание параметров одноименной функции - prophet(), с помощью которой выполняется подгонка моделей. Приведены также подробные примеры использования нескольких параметров, определяющих гладкость компонентов моделей.Код для воспроизведения примеров
Все примеры из этого, а также других сообщений о пакете Prophet, можно воспроизвести с помощью кода, который хранится в Github-репозитории ranalytics/intro_to_prophet. Скопируйте этот код на свой компьютер любым из стандартных в таких случаях способов (см. здесь или здесь).
Аргументы функции prophet()
- df - Необязательный аргумент, с помощью которого указывают таблицу с историческими данными. Такая таблица должна содержать как минимум два столбца: ds (даты в формате YYYY-MM-DD) и y (значения моделируемого отклика). В случаях, когда тренд в y моделируется как логистический рост, таблица с историческими данными должна также содержать столбец cap ("емкость"), который соответствует максимально достижимым значениям y для соответствующих дат. Если аргумент df не указан (NULL), то произойдет только инициализация модельного объекта, а для непосредственного запуска подгонки модели необходимо будет воспользоваться функцией fit.profit(m, df).
- growth - Тип тренда. Принимает два возможных значения - "linear" ("линейный" - принято по умолчанию) и "logistic" ("логистический").
- changepoints - текстовый вектор с датами (в формате "YYYY-MM-DD"), соответствующими "переломным моментам", или "точкам излома" в y (т.е., датам, когда, как предполагается, произошли существенные изменения в тренде временного ряда). Если этот вектор не указан, то такие переломные моменты будут оценены автоматически.
- n.changepoints - предполагаемое количество "переломных моментов" (25 по умолчанию). Если аргумент changepoints задан, то аргумент n.changepoints будет проигнорирован. Если же changepoints не задан, то n.changepoints потенциальных точек излома будут распределены равномерно в пределах исторического отрезка, задаваемого аргументом changepoint.range.
- changepoint.range - доля исторических данных (начиная с самого первого наблюдения), в пределах которых будут оценены точки излома. По умолчанию составляет 0.8 (т.е. 80% наблюдений).
- yearly.seasonality - Параметр настройки годовой сезонности (т.е. закономерных колебаний в пределах года). Принимает следующие возможные значения: "auto" (автоматический режим, принят по умолчанию), TRUE, FALSE или количество членов ряда Фурье, с помощью которого аппроксимируется компонент годовой сезонности.
- weekly.seasonality - Параметр настройки недельной сезонности (т.е. закономерных колебаний в пределах недели). Возможные значения те же, что и у yearly.seasonality.
- daily.seasonality - Параметр настройки дневной сезонности (т.е. закономерных колебаний в пределах дня). Возможные значения те же, что и у yearly.seasonality.
- holidays - Таблица, содержащая два обязательных столбца: holiday (текстовая переменная - названия "праздников" и других важных событий, потенциально влияющих на свойства временного ряда) и ds (даты). По желанию в такую таблицу можно добавить еще два столбца - lower_window и upper_window, которые задают отрезок времени вокруг соответствующего события. Так, например, при "lower_window = -2" в модель будут добавлены 2 дня, предшествующие соответствующему событию. Также по желанию можно добавить столбец prior_scale - априорное значение стандартного отклонения (нормального) распределения, с помощью которого моделируется эффект того или иного события.
- seasonality.mode - Режим моделирования сезонных компонентов. Принимает два возможных значения: "additive" (аддитивный, принят по умолчанию) и "multiplicative" (мультипликативный).
- seasonality.prior.scale - Параметр, задающий "силу" сезонных компонентов модели (10 по умолчанию). Более высокие значения приведут к более "гибкой" модели, а низкие - к модели со слабее выраженными сезонными эффектами. Этот параметр можно задать отдельно для каждого типа сезонности с помощью функции add_seasonality().
- holidays.prior.scale - Параметр, задающий выраженность эффектов "праздников" и других важных событий (10 по умолчанию). Если таблица, подаваемая на аргумент holidays, имеет столбец prior_scale (см. выше), то аргумент holidays.prior.scale будет проигнорирован.
- changepoint.prior.scale - Параметр, задающий "гибкость" автоматического механизма обнаружения "переломных моментов" в y (0.05 по умолчанию). Более высокие значение позволят иметь больше таких точек излома.
- mcmc.samples - Целое число (0 по умолчанию). Если >0, то параметры модели будут оценены путем полного байесовского анализа с использованием mcmc.samples итераций алгоритма MCMC.
- interval.width - Число, определяющее ширину доверительного интервала для предсказанных моделью значений (0.8 по умолчанию, что соответствует 80%-ному интервалу). При "mcmc.samples = 0" этот интервал будет оценен с использованием MAP-метода и только на основе неопределенности в отношении тренда в у. Если же "mcmc.samples > 0", то доверительные интервалы будут оцениваться с учетом неопределенности в отношении оценок всех параметров модели (включая сезонные компоненты).
- uncertainty.samples - Количество итераций для оценивания доверительных интервалов (1000 по умолчанию).
- fit - Логическое значение (TRUE по умолчанию). При "fit = FALSE" произойдет только инициализация модельного объекта, но не подгонка самой модели.
- ... - дополнительные параметры, которые передаются на функцию fit.prophet().
Точки излома тренда
Как отмечено выше, аналитик может задать точки излома либо самостоятельно (с помощью аргумента changepoints), либо довериться их автоматическому обнаружению. Рассмотрим, как работает каждый из этих режимов, и что происходит в результате изменения соответствующих аргументов функции prophet().
В автоматическом режиме при инициализации модели 25 потенциальных точек излома будут равномерно распределены в пределах интервала, который охватывает первые 80% наблюдений из обучающей выборки. Именно это произошло, когда мы построили нашу базовую модель М0 (см. предыдущее сообщение). Однако эти 25 точек - лишь предполагаемые места существенных изменений в тренде: в большинстве случаев на практике тренд временного ряда не изменяется так часто. Поэтому в ходе подгонки модели срабатывает механизм регуляризации (подобный L1-регуляризации), в результате чего выбирается минимально необходимое количество точек излома. Изобразить эти автоматически обнаруженные точки излома можно с помощью функции add_changepoints_to_plot(). В случае с моделью M0 имеем:
plot(M0, forecast_M0) + add_changepoints_to_plot(M0)
 |
| Рис. 1. Сплошная красная линия - тренд, оцененный с помощью модели M0. Штриховые красные линии - оцененные точки излома тренда. |
Глядя на исходные данные, можно сделать заключение, что модель M0 все еще переоценивает количество "переломных моментов" в тренде. Построим новую модель, которая будет инициализирована с меньшим начальным количеством потенциальных точек излома (15 вместо 25 - см. аргумент n.changepoints):
# Подгонка модели:
M1 <- prophet(train_df, n.changepoints = 15)
# Расчет прогноза:
forecast_M1 <- predict(M1, future_df)
# Графическое представление оцененных точек излома тренда:
plot(M1, forecast_M1) + add_changepoints_to_plot(M1)
 |
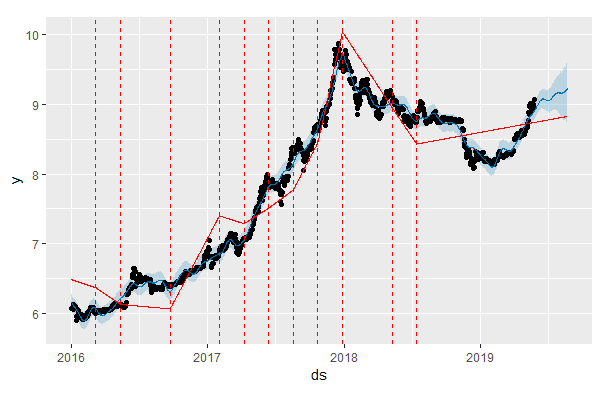| Рис. 2 |
Как и ожидалось, оцененный тренд получился более сглаженным, чем в модели M0. Хорошо это или плохо, мы узнаем позже, когда рассмотрим способ диагностики качества Prophet-моделей с помощью перекрестной проверки.
Помимо изменения начального количества потенциальных точек излома тренда, мы можем также изменить интервал времени, в пределах которого происходит их оценивание. По умолчанию этот интервал охватывает первые 80% наблюдений. Однако из приведенных выше графиков видно, что примерно в начале ноября 2018 г. произошло резкое падение стоимости биткоина (о причине этого см. здесь). Ни одна из построенных нами моделей пока не "уловила" это изменение, поскольку оно не вошло в интервал, в пределах которого оцениваются точки излома. Увеличим этот интервал до 90%, воспользовавшись аргументом changepoint.range (одновременно увеличим количество потенциальных точек излома с 15 до 20, поскольку на большем промежутке времени можно ожидать больше "перепадов" в тренде):
# Подгонка модели:
M2 <- prophet(train_df, n.changepoints = 20, changepoint.range = 0.9)
# Расчет прогноза:
forecast_M2 <- predict(M2, future_df)
# Графическое представление оцененных точек излома тренда:
plot(M2, forecast_M2) + add_changepoints_to_plot(M2)
 |
| Рис. 3 |
Полученная модель M2 намного лучше передает свойства анализируемого временного ряда. Это касается и получаемого с ее помощью прогноза (как с точки зрения направления тренда, так и с точки зрения ширины доверительных интервалов предсказанных значений).
changepoint.prior.scale - это еще один параметр который позволяет настроить гладкость тренда в моделируемом временном ряду. Чем больше значение этого параметра (по сравнению с принятым по умолчанию значением 0.05), тем больше точек излома останется в подогнанной модели. Рассмотрим эффект действия этого параметра на примере следующей модели:
# В этой модели мы увеличиваем интервал, в пределах которого
# оцениваются точки излома тренда (до 90%), одновременно увеличивая
# уровень регуляризации с помощью параметра changepoint.prior.scale.
# Начальное количество потенциальных точек излома оставим равным значению,
# принятому по умолчанию (25):
# Подгонка модели:
M3 <- prophet(train_df,
changepoint.range = 0.9,
changepoint.prior.scale = 0.02)
# Расчет прогноза:
forecast_M3 <- predict(M3, future_df)
# Графическое представление оцененных точек излома тренда:
plot(M3, forecast_M3) + add_changepoints_to_plot(M3)
 |
| Рис. 4 |
Как видим, модели M2 и M3 дают похожие результаты, что скорее определяется значением параметра changepoint.range, нежели способом регуляризации количества точек излома.
Наконец, посмотрим, что получится, если задать точки излома тренда "вручную", а не оценивать их в автоматическом режиме. Для этого служит аргумент changepoints:
# В этой модели мы задаем точки излома тренда самостоятельно
# (выбор дат, подаваемых на аргумент changepoints, основан на
# визуальном анализе исходных данных):
# Подгонка модели:
M4 <- prophet(train_df,
changepoints = c("2016-04-01",
"2016-06-15",
"2016-10-01",
"2017-04-01",
"2017-07-01",
"2017-09-01",
"2017-12-26",
"2018-04-01",
"2018-11-13",
"2018-12-15",
"2019-04-01"))
# Расчет прогноза:
forecast_M4 <- predict(M4, future_df)
# Графическое представление оцененных точек излома тренда:
plot(M4, forecast_M4) + add_changepoints_to_plot(M4)
 |
| Рис. 5 |
Модель M4 хорошо описывает тренд в анализируемом временном ряду, хотя не исключено что она несколько переобучена (выяснить так ли это нам поможет диагностика с помощью перекрестной проверки, которой будет посвящено одно из следующих сообщений).
Гладкость сезонных компонентов
Сезонные компоненты аппроксимируются в Prophet с помощью частичныx сумм ряда Фурье (подробнее см. Taylor & Letham 2017). Число членов ряда ("порядок ряда") является параметром, который определяет скорость изменения того или иного компонента. Так, для (внутри-)годовой сезонности порядок ряда по умолчанию составляет 10. В случае с моделью M4 это приводит к следующему компоненту годовой сезонности (обратите внимание на использование скрытой функции plot_yearly(), которую можно вызвать только обычным в таких случаях образом, т.е. указав имя пакета в сочетании с тройным двоеточем перед именем скрытой функции):
prophet:::plot_yearly(M4)
 |
| Рис. 6 |
С помощью аргумента yearly.seasonality можно изменить гладкость компонента годовой сезонности. В приведенном ниже примере значение этого аргумента увеличено с заданного по умолчанию 10 до 20, что привело к менее гладкой кривой:
M4B <- prophet(train_df,
yearly.seasonality = 20,
changepoints = c("2016-04-01",
"2016-06-15",
"2016-10-01",
"2017-04-01",
"2017-07-01",
"2017-09-01",
"2017-12-26",
"2018-04-01",
"2018-11-13",
"2018-12-15",
"2019-04-01"))
prophet:::plot_yearly(M4B)
 |
| Рис. 7 |
Аналогичным образом можно изменить гладкость компонентов недельной (weekly.seasonality) и дневной сезонности (daily.seasonality).
В этой статье мы рассмотрели несколько параметров функции prophet(), задающих гладкость компонентов моделей. В следующем сообщении мы продолжим знакомство с параметрами этой функции и познакомимся со способами моделирования эффектов "праздников" и других важных событий, влияющих на свойства временного ряда.
Отправить комментарий