Автор: Владимир Шитиков
Введение
Пусть изучаемая случайная величина \(\boldsymbol{X}\) распределена по неизвестному закону. Тогда по репрезентативной выборке \(X\) объемом \(n\) можно построить две эмпирические функции распределения: функцию плотности вероятности PDF (Probability Density Function) и кумулятивную функцию распределения CDF (Cumulative Distribution Function). Если методы построения PDF широко распространены и легко реализуются в R в форме ядерной функции сглаживания density(), то построение и анализ кумулятивных кривых распределения имеет ряд характерных особенностей, обсуждаемых ниже.
Эмпирическая CDF является непараметрической оценкой неизвестной
генеральной функции распределения случайной величины. При ее построении
выборку \(X\) предварительно сортируют по возрастанию наблюдаемых величин, каждому исходному элементу присваивают значения вероятности 1/n, и далее на каждом шаге с использованием интерполяции вычисляют сумму этих вероятностей:
n <- length(x) x <- sort(x); vals <- unique(x) rval <- approxfun(vals, cumsum(tabulate(match(x, vals)))/n, method = "constant", yleft = 0, yright = 1, f = 0, ties = "ordered")
Эмпирическая CDF математически определяется как
\[\hat{F}_n (x) = \hat{P}_{n(X \leq x)} = n^{-1} \sum_{i=1}^{n} \boldsymbol{I} (x_{i} \leq x), \]
где \(\boldsymbol{I}\) - индикаторная функция, принимающая два возможных значения:
\(I(x_i \leq x) = \begin{cases} 1,&\text{если }x_i \leq x\\ 0,&\text{если }x_i > x \end{cases}\)
Согласно теореме Гливенко-Кантелли, \(\hat{F}_n (x)\) является состоятельной оценкой \(F_n (x)\) и равномерно сходится к ней при \( n \to \infty \).
На практике построение эмпирической CDF может оказаться полезным по следующим причинам:
- если совокупный размер исходных выборок достаточно велик, то CDF является аппроксимацией "истинной" функции распределения, что может быть полезным для проверки статистических гипотез;
- график эмпирической CDF можно визуально сравнить с аналогичными кривыми для часто используемых теоретических распределений и проверить, не распределена ли случайная величина по известному закону;
- CDF может графически отобразить насколько "быстро" (с оценкой коэффициента угла наклона отрезков прямых на графике) вероятности увеличиваются от 0 до 1;
- выделение основных квантилей, таких, например, как {0.025, 0.25, 0.5, 0.75, 0.975}, позволяет лучше понять характер вариации данных.
Формирование, отображение и сглаживание эмпирических функций распределения
Используем в качестве примера набор данных endosulfan, входящий в состав пакета fitdistrplus, и содержащий 104 показателя острой токсичности ATV (мкг/л) для хлорорганического пестицида эндосульфана. Данные токсикометрического эксперимента представлены для трех групп различных водных организмов, включая членистоногих (Art), рыб (Fis) и беспозвоночных (Non). Поскольку для экотоксикологических данных часто характерно логнормальное распределение, значения ATV предварительно прологарифмируем. Отдельно выделим набор показателей для 34 видов членистоногих:
library(fitdistrplus) data(endosulfan) ATVlog <- data.frame(ATV = log10(endosulfan$ATV), group = substr(endosulfan$group, 1, 3)) levels(ATVlog$group) # [1] "Art" "Fis" "Non" ATV.Art <-subset(ATVlog,group == "Art")$ATV
Графически эмпирическая кривая CDF может быть представлена в трех форматах: (а) в виде последовательности жирных точек с "закорючками", характерных для функции ecdf(); (б) в виде кусочно-ступенчатой линии с использованием функции stat_ecdf() из пакета ggplot2 и (в) в виде ломаной прямой, проходящей через эмпирические точки, либо позиции Хазена (Hazen 1919), т.е. точки значений вероятности, расположенные на половине высоты каждой "ступеньки". Покажем эти форматы кривых на графике, используя значения ATV для членистоногих:
# сортировка данных по Arthropods ATV.Art = sort(ATV.Art) (n = length(ATV.Art)) # [1] 34 plot(ecdf(ATV.Art), xlab= "Концентрация эндосульфана (логарифм)") lines (ATV.Art, (1:n)/n, type = 's', col="blue") uniDF <- data.frame(ATV = unique(ATV.Art), r = as.vector(table(ATV.Art))) pHazen = cumsum(uniDF$r)/n - uniDF$r*0.5/n lines (uniDF$ATV, pHazen, type = 'o', lwd=1, cex=0.7, col="red")
Для статистических расчетов при \(n \gt 15\) вид кривой CDF имеет лишь эстетическое значение, поскольку параллельное смещение различных вариантов ее отображения варьирует в пределах, не превышающих 1/30 = 0.033 размаха шкалы ординат. Отметим также, что упоминаемая в литературе (Delignette-Muller 2015) формула (1:n - 0.5)/n для позиций Хазена справедлива лишь в случае неповторяющихся значений \(X\), и поэтому для нашего примера была откорректирована.
Роль представленной CDF в экотоксикологии весьма велика, т.к. она определяет статистическую модель распределения чувствительности видов SSD (Species Sensitivity Distribution). Она задает последовательность критических концентраций токсиканта \(HC_{p}\), которые будут опасными для р% наиболее чувствительных видов и неэффективными для остальных. Например, по полученной кривой легко установить, что при концентрации эндосульфана 10 мкг/л (т.е. при \(\log (10) = 1\)) имеется риск гибели около 57% видов членистоногих (раков, крабов и т.д.). Или, наоборот, задавшись допустимым значением эмпирического риска р = 0.1 (т.е. мы заранее согласны с гибелью 10% видов) можно получить пороговую опасную концентрацию \(HC_{0.1}\)= 0.33 мкг/л.
Ступенчатая, или кусочно-линейная форма кумулятивной кривой CDF иногда вызывает "чувство неприятия" у аналитиков, привыкших к прямолинейным или плавным криволинейным зависимостям. В этом случае, как будет показано далее, можно воспользоваться различными функциями сглаживания: локальной регрессией, полиномами, сплайнами или ядерными функциями. Здесь необходимо иметь в виду, что подобные попытки аппроксимации могут привести к серьезным и непредсказуемым скачкам функции распределения плотности вероятности PDF, восстановленной по сглаженной CDF, поскольку PDF очень чувствительна даже к небольшим модификациям CDF.
Более осторожный подход связан с предварительной аппроксимацией PDF некоторой подходящей функцией, по которой затем строится сглаженная эмпирическая кумулятивная функция. Рассмотрим два метода, первый из которых связан с построением CDF на основе гистограммы.
Разделим интервал варьирования наблюдаемой величины на шесть классов токсичности по уровню концентрации эндосульфана и построим кусочно-линейную функцию кумулятивного распределения вероятностей, состоящую из небольшого числа участков.
par(mar = c(5,5,2,5)) h <- hist(ATV.Art, breaks = 4, freq = FALSE, col = "lightblue", xlab= "Концентрация эндосульфана (логарифм)") lines(density(ATV.Art), col = "red", lwd = 2) par(new = TRUE) ec <- ecdf(ATV.Art) plot(x = h$mids, y = ec(h$mids) * max(h$counts), col = rgb(0, 0, 0, alpha = 0), axes = FALSE, xlab = NA, ylab = NA) lines(x = h$mids, y = ec(h$mids) * max(h$counts), col = 'blue', lwd = 2) axis(4, at = seq(from = 0, to = max(h$counts), length.out = 11), labels = seq(0, 1, 0.1), col = 'blue', col.axis = 'blue') mtext(side = 4, line = 3, 'Cumulative Density', col = 'blue')
Представленный метод эффективен для выявления закономерностей распределения в больших зашумленных массивах данных (n > 500). Другой метод основан на использовании PDF, которая аппроксимируется ядерной функцией. Переход от непрерывных значений плотности распределения к непрерывной форме ЕCDF удобно осуществить с помощью функций geom_density() и stat_ecdf() из пакета ggplot2:
smooth_ecd = function(adj = 1) { # Оценка ядерной плотности по эмпирическим данным dens = density(dat$x, adjust = adj) dens = data.frame(x = dens$x, y = dens$y) # График ядерной плотности (синий), # ecdf (черный) и сглаженной ecdf (красный) ggplot(dat, aes(x)) + geom_density(adjust = adj, colour = "blue", alpha = 0.7) + geom_line(data = dens, aes(x = x, y = cumsum(y)/sum(y)), size = 1, colour = 'red') + stat_ecdf(colour = "black", size = 0.6, alpha = 0.6) + theme_classic() + labs(title=paste0("adj=",adj)) } library(ggplot2) dat <- data.frame(x = ATV.Art) smooth_ecd(adj = 1) smooth_ecd(adj = 0.3)
Методически более осмысленной процедурой является подгонка эмпирического распределения одним из известных теоретических распределений (Delignette-Muller 2015). Используем для этого функции из пакетов fitdistrplus и actuar:
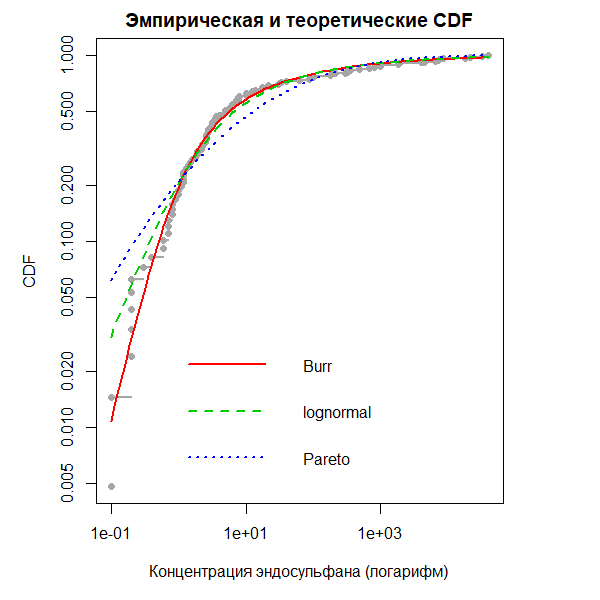
library("actuar") ATV <- endosulfan$ATV fendo.ln <- fitdist(ATV, "lnorm") fendo.P <- fitdist(ATV, "pareto", start = list(shape = 1, scale = 500)) fendo.B <- fitdist(ATV, "burr", start = list(shape1 = 0.3, shape2 = 1, rate = 1)) cdfcomp(list(fendo.B, fendo.P, fendo.ln), lwd=2, xlogscale = TRUE, ylogscale = TRUE, datacol = "gray65", main = "Эмпирическая и теоретические CDF", xlab = "Концентрация эндосульфана (логарифм)", legendtext = c("Burr","lognormal","Pareto"))
gofstat(list(fendo.B, fendo.P, fendo.ln)) # Goodness-of-fit statistics # 1-mle-burr 2-mle-pareto 3-mle-lnorm # Kolmogorov-Smirnov statistic 0.06154925 0.08488002 0.1672498 # Cramer-von Mises statistic 0.06803071 0.13926498 0.6373593 # Anderson-Darling statistic 0.52393018 0.89206283 3.4721179 # Goodness-of-fit criteria # 1-mle-burr 2-mle-pareto 3-mle-lnorm # Aikake Information Crit 1045.731 1048.112 1068.810 # Bayesian Information Crit 1053.664 1053.400 1074.099 approx.ksD <- function(n) { ## оценка критического значения статистики Колмогорова- ## Смирнова D для доверительного уровня 0.95. ## реализована по Bickel & Doksum, table IX, p.483 ## и Lienert G.A.(1975) ifelse(n > 80, 1.358 /( sqrt(n) + .12 + .11/sqrt(n)), ##B&D splinefun(c(1:9, 10, 15, 10 * 2:8),# from Lienert c(.975, .84189, .70760, .62394, .56328, # 1:5 .51926, .48342, .45427, .43001, .40925, # 6:10 .33760, .29408, .24170, .21012, # 15,20,30,40 .18841, .17231, .15975, .14960)) (n)) } approx.ksD(length(ATV)) # [1] 0.1314767
Статистика Колмогорова-Смирнова D равна максимуму различий между эмпирической и теоретической кумулятивными кривыми распределений:
\[D_{n}=\sup_{x}|\hat{F}_{n}(x) - F(x)|,\]
где \(\sup \) - супремум множества расстояний. По теореме Гливенко-Кантелли, если выборка получена из распределения \(\boldsymbol{F}(x)\), то \(D_n\) сходится к 0.
Поскольку вычисленные выше значения статистики Колмогорова-Смирнова для распределений Бара и Парето не превышают критического, то с риском ошибиться менее 5% мы принимаем гипотезу о принадлежности к любому из этих распределений. Если подгонка известными теоретическими распределениями не достигает необходимой точности, то можно попробовать подобрать смесь из нескольких распределений с использованием функции UnivarMixingDistribution() из пакета distr.
Сравнение CDF некскольких выборок
Для упомянутых выше трех групп водной фауны построим распределения плотности вероятности PDF. Синими пунктирными линиями покажем положения квартильных значений среднелетальных концентраций эндосульфана.
ggplot(ATVlog) + aes(ATV, fill = group) + labs(x = 'Концентрация эндосульфана (логарифм)', y = 'Плотность вероятности') + geom_density(alpha = 0.3)+ geom_vline(xintercept = quantile(ATVlog$ATV, p = c(0.25, 0.5, 0.75)), colour = "blue", linetype = 5, size = 1)+ theme_bw()
Здесь и на последующих рисунках розовым цветом обозначены членистоногие (Art), зеленым - рыбы (Fis) и голубым - беспозвоночные (Non).
Построим теперь кривые чувствительности видов (т.е. графики CDF). Найдем и отметим на полученном графике положения максимальных расстояний между кривыми, соответствующими разным группам животных:
# Функция, формирующая профиль разностей двух ECDF decdf <- function(x, a, b) ecdf(a)(x) - ecdf(b)(x) ATV.Fis <-subset(ATVlog,group == "Fis")$ATV ATV.Non <-subset(ATVlog,group == "Non")$ATV ATV.Un <- sort(ATVlog$ATV) ; ATV.Un <- unique(ATV.Un) x12 <- ATV.Un[which.max(decdf(ATV.Un,ATV.Art, ATV.Fis))] x21 <- ATV.Un[which.min(decdf(ATV.Un,ATV.Art, ATV.Fis))] x13 <- ATV.Un[which.max(decdf(ATV.Un,ATV.Art, ATV.Non))] x23 <- ATV.Un[which.max(decdf(ATV.Un,ATV.Fis, ATV.Non))] cdf.Art <-ecdf(ATV.Art) ; cdf.Fis <-ecdf(ATV.Fis) cdf.Non <-ecdf(ATV.Non) ggplot(ATVlog, aes(x = ATV, color = group))+ labs(x = 'Концентрация эндосульфана (логарифм)', y = 'Накопленная вероятность') + stat_ecdf(geom = "step", size = 1) + theme_bw() + geom_segment(aes(x = x12, y = cdf.Art(x12), xend = x12, yend = cdf.Fis(x12)), linetype = "dashed",size=1, colour = "black" ) + geom_segment(aes(x = x21, y = cdf.Art(x21), xend = x21, yend = cdf.Fis(x21)), linetype = "dashed",size=1, colour = "black" ) + geom_segment(aes(x = x13, y = cdf.Art(x13), xend = x13, yend = cdf.Non(x13)),linetype = "dashed",size=1, colour = "black" ) + geom_segment(aes(x = x23, y = cdf.Non(x23), xend = x23, yend = cdf.Fis(x23)), linetype = "dashed",size=1, colour = "black" )
\[ D_{n, m} = \ sup_{x} | \hat{F}_{1, n} (x) - \hat{F}_{2, m} (x) |.\]
Нулевая гипотеза, утверждающая, что обе выборки взяты из одного и того же распределения, отклоняется на уровне \(\alpha\), если
\[ D_{n, m} > c (\alpha) {\sqrt {\frac {n + m} {nm}}},\]
где \( c\left(\alpha \right)={\sqrt {-{\frac{1}{2}}\ln \left({\frac{\alpha }{2}}\right)}}\).
Выполним попарное сравнение групп гидробионтов и проверим три нулевых гипотезы об эквивалентности CDF (alternative = "two.sided"). Отметим, что функции для членистоногих и рыб пересекаются, и поэтому необходимо еще проверить гипотезу о том, какая из кривых располагается выше другой ("less" или "greater"):
# Двухвыборочный тест Колмогорова-Смирнова ks.ts <- ks.test(ATV.Art, ATV.Fis, alternative = "two.sided") # data: ATV.Art and ATV.Fis # D = 0.3627, p-value = 0.00825 # alternative hypothesis: two-sided ks.lt <- ks.test(ATV.Art, ATV.Fis, alternative = "less") # D^- = 0.3627, p-value = 0.004125 # alternative hypothesis: the CDF of x lies below that of y ks.gt <- ks.test(ATV.Art, ATV.Fis, alternative = "greater") # D^+ = 0.098, p-value = 0.6696 # alternative hypothesis: the CDF of x lies above that of y ks.ts13 <- ks.test(ATV.Art, ATV.Non, alternative = "two.sided") # data: ATV.Art and ATV.Non # D = 0.7537, p-value = 8.571e-06 # alternative hypothesis: two-sided ks.ts23 <- ks.test(ATV.Fis, ATV.Non, alternative = "two.sided") # data: ATV.Fis and ATV.Non # D = 0.9074, p-value = 2.976e-09 # alternative hypothesis: two-sided print(p.adjust(c(ks.ts$p.value, ks.ts13$p.value, ks.ts23$p.value), "bonferroni")[1], 4) # [1] 2.4750e-02 2.5713e-05 8.9280e-09
Последним действием с использованием поправки Бонферрони мы оценили уровень значимости каждой из составляющих множественной гипотезы о том, что все три CDF эквивалентны. Поскольку все нулевые гипотезы отклоняются с высоким уровнем значимости, то предположение об одном генеральном распределении для всех трех выборок и одинаковой чувствительности к токсиканту трех групп водных организмов следует отвергнуть.
Существует несколько вариантов построения доверительной полосы (confidence band) для CDF. Один из них основан на неравенстве Дворецкого-Кифера-Вольфовица (ДКВ, Dvoretzky–Kiefer-Wolfowitz, 1956), которое определяет, насколько близко эмпирическая функция распределения связана с функцией распределения, из которой извлекаются эмпирические выборки:
\[Pr(\text{sup}|\hat{F}_n(x) - F(x)| > \epsilon) \leq 2\exp(-2n\epsilon^2),\]
где \(\epsilon\) - некоторая положительная постоянная.Если принять уровень значимости \(\alpha = 2 \exp (-2n\times \epsilon^2) \), то \(\epsilon (n) =[\log (2 / \alpha) / (2n)]^{0.5} \). Используя неравенство ДКВ и представленное выражение для \(\epsilon\), можно оценить доверительные интервалы (CI) для \(\boldsymbol{F}(x)\):
\[CI_{l,u} = \hat{F}_n(x) \pm \epsilon,\]
которые будут находиться на одинаковом удалении от каждой точки ECDF по оси ординат.
Более точно значение \(\epsilon\) можно оценить с помощью аппроксимации статистики Колмогорова-Смирнова (КС) вышеприведенной функцией approx.ksD(). Заинтересованные читатели могут воспользоваться также функцией ecdf.ksCI() из пакета sfsmisc, в которой заложен именно этот алгоритм.
Более точно значение \(\epsilon\) можно оценить с помощью аппроксимации статистики Колмогорова-Смирнова (КС) вышеприведенной функцией approx.ksD(). Заинтересованные читатели могут воспользоваться также функцией ecdf.ksCI() из пакета sfsmisc, в которой заложен именно этот алгоритм.
Второй вариант основан на том, что согласно центральной предельной теореме (ЦПТ) асимптотическое поточечное распределение абсолютной разности \(\boldsymbol{F}(x)\) и \(\hat{F}_n(x)\) имеет нормальное распределение со стандартной степенью приближения \[\sqrt{n}(\hat{F}_n(x)-F(x)) \rightarrow \mathcal{N}(0,F(x)(1-F(x))).\]
Поскольку \(E(\hat{F}_n(x)) = \boldsymbol{F}(x)\), мы можем оценить доверительную полосу для \(\boldsymbol{F}(x)\), имеющую переменное значение в каждой точке ECDF:
\[\hat{F}_n(x) \pm z_{\alpha} \frac{\hat{F}_n(x)(1-\hat{F}_n(x))}{n}.\]
Рассмотрим код для построения графика доверительных огибающих:# Функция, формирующая доверительные интервалы ECDF get_df.ecdf <- function(x, group, level = 0.05) { n <- length(x) x.sort <- sort(x) y <- (1:n)/n # CI по теореме Дворецкого-Кифера-Вольфовица (ДКВ) epsilon = sqrt(log(2/level)/(2*n)) L = pmax(y - epsilon, 0) U = pmin(y + epsilon, 1) D <- approx.ksD(n) U3 <- pmin(y + D, 1) L3 <- pmax(y - D, 0) # CI на основе центральной предельной теоремы (ЦПТ) z <- qnorm(1-level/2) U2 = pmin(y + z*sqrt(y*(1-y)/n ),1) L2 = pmax(y - z*sqrt(y*(1-y)/n ),0) data.frame(x=x.sort, y, group, L, U, L2, U2, L3, U3) } # Формирование объединенной таблицы df.Art <- get_df.ecdf(ATV.Art,"Art") df.all <- rbind(df.Art, get_df.ecdf(ATV.Fis,"Fis")) df.all <- rbind(df.all, get_df.ecdf(ATV.Non,"Non")) # Создание графика library(ggplot2) ggplot(df.all, aes(x=x, y=y)) + # Эмпирические распределения geom_line(aes(colour=group),size=1.2) + # Заливаются области доверительных интервалов ДКВ geom_ribbon(aes(ymin = L, ymax = U, fill = group), alpha = 0.5) + geom_line(aes(x = x, y = L3, colour = group), linetype = "3313", size = 1) + geom_line(aes(x = x, y = U3, colour = group), linetype = "3313", size = 1) + # Рисуются кривые доверительных интервалов ЦПТ geom_line(aes(x = x, y = L2, colour = group), linetype = "dashed", size = 1) + geom_line(aes(x = x, y = U2, colour = group), linetype = "dashed", size = 1) + labs(x = 'Концентрация эндосульфана (логарифм)', y = 'Накопленная вероятность') + theme_bw()
Здесь сплошными линиями показаны эмпирические CDF для каждой группы организмов с 95% доверительной областью ДКВ, залитой соответствующим цветом. Штрих-пунктирными линиями отмечены границы, полученные с помощью аппроксимации КС, а штриховыми линиями - полученные с применением ЦПТ.
Третьим способом оценки доверительных интервалов является непараметрическая бутстреп-процедура. Для этого на основе имеющейся эмпирической выборки генерируется множество псевдовыборок того же размера, состоящих из случайных комбинаций исходного набора элементов. При этом используется алгоритм "случайного выбора с возвращением" (random sampling with replacement), т.е. извлеченный выборочный элемент снова помещается в исходную совокупность, прежде чем извелекается следующее наблюдение. В результате некоторые наблюдения в каждой отдельной бутстреп-выборке могут повторяться два или более раз, тогда как другие - отсутствовать.
Для каждой бутстреп-выборки формируется кумулятивная функция распределения, а доверительная полоса в каждом ее вертикальном сечении включает "пучок" из 95% таких кривых, максимально приближенных к медиане. Ограничимся 200 репликами и выполним расчеты только для группы членистоногих:
n = length(ATV.Art) nrep = 200 # новые данные для построения плавной кривой newxs <- (seq(min(ATV.Art), max(ATV.Art), length.out = 100)) # добавление в итоговую таблицу координат ECDF pdat <- data.frame(newxs, py = ecdf(ATV.Art)(newxs)) # создание бутстреп-выборок boots <- t(replicate(nrep, ATV.Art[sample.int(n, replace = TRUE)])) bootdat <- data.frame(apply(boots, 1, function(x) ecdf(x)(newxs))) # извлечение доверительных интервалов cis <- apply(bootdat, 1, quantile, c(0.025, 0.975)) rownames(cis) <- c('lwr', 'upr') # добавление доверительных интервалов pdat <- cbind(pdat, t(cis)) # таблица бустреп-кривых bootdat$newxs <- newxs require(reshape2) bootline <- melt(bootdat, id = 'newxs') # Вывод итогового графика с использованием пакета ggplot2 library(ggplot2) ggplot()+ labs(x = 'Концентрация эндосульфана (логарифм)', y = 'Накопленная вероятность') + geom_line(data = bootline, aes(x = newxs, y = value, group = variable), col = 'steelblue', alpha = 0.5) + geom_smooth(data = pdat, aes(x = newxs, y = py), col = 'red', size=1.2, se= FALSE) + geom_smooth(data = pdat, aes(x = newxs, y = lwr), linetype = 'dashed', size=1.2, se= FALSE) + geom_smooth(data = pdat, aes(x = newxs, y = upr), linetype = 'dashed', size=1.2, se= FALSE) + geom_smooth(data = df.Art, aes(x = x, y = L), linetype = '3313', col = 'green',size=1, se= FALSE) + geom_smooth(data = df.Art, aes(x = x, y = U), linetype = '3313', col = 'green',size=1, se= FALSE) + theme_bw()
Здесь ступенчатыми линиями показаны CDF на основе бутстреп-выборок. Остальные представленные кривые были сглажены локальной регрессией, в том числе: красным цветом показана эмпирическая CDF, синие штриховые линии обозначают доверительные огибающие, полученные бутстреп-методом, а зеленые штрих-пунктирные - доверительные огибающие, полученные из неравенства Дворецкого-Кифера-Вольфовица (приведены для сравнения).
Видно, что доверительные области, построенные на основе ЦПТ и бутстреп-метода существенно уже, чем ДКВ-области, особенно на обоих концах кумулятивной кривой. Как следует из дискуссии, это - два разных типа доверительных полос. "Точечная доверительная полоса" (pointwise confidence band) предполагает, что, если выборки данных извлекаются из некоторого генерального распределения, то в среднем 5% точек окажется вне доверительной области. Для "одновременной полосы" (simultaneous band) формулируется принципиально иное условие: существует 5%-ная вероятность того, что точка с наибольшим отклонением окажется вне доверительной области (Francisco-Fernandez & Quintela-del-Rio 2016).
Благодарности
Выражаю искреннюю
признательность своему многолетнему знакомому, математику-статистику Н. А.
Цейтлину (г. Гамбург), за плодотворное обсуждение и ценные замечания.
Список литературы
- Delignette-Muller ML (2015) fitdistrplus: An R package for fitting distributions. Journal of Statistical Software 64(4)
- Francisco-Fernandez M, Quintela-del-Rio A (2016) Comparing simultaneous and pointwise confidence intervals for hydrological processes. PLoS ONE 11: 2-28
- Цейтлин НА, Горбач АН (2015) Маркетинговое исследование телевизионной рекламной кампании интернет-магазина. Харьков: Impress, 111 с. PDF .








Отправить комментарий