Дисперсионный анализ: проверка адекватности модели

Как было показано ранее, дисперсионный анализ представляет собой частный случай общей линейной модели. Оценить параметры такой модели и их значимость позволяет базовая R-функция lm() (см. примеры здесь и здесь). Однако подгонкой модели анализ не заканчивается. Перед тем, как интерпретировать рассчитанные параметры и их Р-значения, необходимо проверить адекватность модели (англ. model adequacy), т.е. выяснить, выполняются ли лежащие в ее основе допущения (англ. model assumptions). Ниже рассмотрены условия применимости классического однофакторного дисперсионного анализа.

Постановка проблемы

В качестве примера используем данные эксперимента по изучению эффективности 6 разных инсектицидов (таблица InsectSprays с этими данными входит в состав базовой версии R; см. также здесь и здесь). Каждым из этих средств обработали по 12 растений, после чего подсчитали количество выживших на растениях насекомых. Нулевая гипотеза, которую мы проверим при помощи дисперсионного анализа, заключается в том, что исследованные инсектициды не различаются по эффективности (т.е. наблюдаемые различия в групповых средних значениях числа выживших насекомых совершенно случайны). Исходные данные выглядят так:

InsectSprays
   count spray
1     10     A
2      7     A
3     20     A
4     14     A
5     14     A
6     12     A
7     10     A
8     23     A
9     17     A
10    20     A
11    14     A
12    13     A
13    11     B
14    17     B
15    21     B
...   ...    ...
69    26     F
70    26     F
71    24     F
72    13     F

Линейную модель, параметры которой нам предстоит оценить, можно записать следующим образом:

\[y_{i} = \beta_0 + \beta_1 x_{i1} + \beta_2 x_{i2} + \beta_3 x_{i3} + \beta_4 x_{i4} + \beta_5 x_{i5} + \epsilon_{i},\]

где \(y_i\) - это число насекомых на i-м растении, \(\beta_0\) - среднее значение числа насекомых для базового уровня изучаемого фактора (по умолчанию R выберет в качестве базового инсектицид А), \(\beta_1\), \(\beta_2\), \(\beta_3\) и т.д. - коэффициенты, отражающие разницу между средним значением числа насекомых на растениях из группы А и средними значениями в других группах (B, C ... F), а \(\epsilon_i\) - остатки модели. Уровни изучаемого фактора закодированы при помощи дополнительной переменной-индикатора x, которая может принимать только два значения - 0 или 1, в зависимости от того, к какому уровню принадлежит конкретное наблюдение \(y_i\) (подробнее о кодировании уровней категориальных предикторов при помощи индикаторных переменных см. здесь и здесь).

Оценим параметры приведенной модели при помощи функции lm():

M <- lm(count ~ spray, data = InsectSprays)
 
summary(M)
 
Call:
lm(formula = count ~ spray, data = InsectSprays)
 
Residuals:
   Min     1Q Median     3Q    Max 
-8.333 -1.958 -0.500  1.667  9.333 
 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  14.5000     1.1322  12.807  < 2e-16 ***
sprayB        0.8333     1.6011   0.520    0.604    
sprayC      -12.4167     1.6011  -7.755 7.27e-11 ***
sprayD       -9.5833     1.6011  -5.985 9.82e-08 ***
sprayE      -11.0000     1.6011  -6.870 2.75e-09 ***
sprayF        2.1667     1.6011   1.353    0.181    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 
Residual standard error: 3.922 on 66 degrees of freedom
Multiple R-squared:  0.7244, Adjusted R-squared:  0.7036 
F-statistic:  34.7 on 5 and 66 DF,  p-value: < 2.2e-16

Интерпретация полученных результатов была подробно описана в одном из предыдущих сообщений. Сейчас для нас наибольший интерес представляет строка в таблице с результатами, обозначенная как F-statistic. В этой строке представлено расчетное значение F-критерия (34.7 при 5 и 66 числах степеней свободы), при помощи которого проверяется гипотеза об одновременном равенстве всех параметров модели нулю. Как видно из соответствующего P-значения этого критерия (p-value: < 2.2e-16), вероятность того, что эта гипотеза верна, крайне мала. Другими словами, мы можем заключить, что эффективность исследованных инсектицидов существенно различается. Вопрос, однако, заключается в том, насколько мы можем доверять полученному F-значению (и его соответствующему Р-значению), чтобы сделать такой вывод? Другими словами, насколько рассчитанное значение F-критерия близко к тому значению, которое следует ожидать, исходя из свойств F-распределения? Это соответствие будет полным при одновременном выполнении следующих трех условий:

• Во всех анализируемых группах (инсектициды A, B, ... F) значения зависимой переменной (число выживших насекомых) должны быть распределены нормально.
• Дисперсия значений зависимой переменной должна быть одинакова во всех группах.
• Во всех группах значения зависимой переменной должны быть независимы.

Для проверки первых двух допущений существуют графические и формальные методы, и ниже мы обсудим их подробнее. Формально проверить (и скорректировать) третье условие сложнее - его выполнение следует обеспечивать на стадии планирования исследования (например, путем случайного назначения каждого растения в ту или иную экспериментальную группу) и в ходе сбора данных (например, используя строго один и тот же метод подсчета насекомых на растениях из всех экспериментальных групп).

Проверка условия нормальности распределения

Важно понимать: условие нормальности в отношении дисперсионного анализа предполагает, что значения зависимой переменной имеют нормальное распределение в пределах каждой группы, определяемой уровнями изучаемого фактора (или факторов) (так, в эксперименте с инсектицидами значения числа выживших насекомых должны быть нормально распределены в каждой из 6 экспериментальных групп). Если изучаемый фактор оказывает существенное влияние на интересующую нас зависимую переменную, то значения этой переменной, взятые все вместе (т.е. без разделения их по группам), совсем необязательно будут иметь нормальное распределение (подробнее см. здесь). Об этом следует помнить при проверке условия нормальности в ходе дисперсионного анализа (т.е. проверять нормальность распределения необходимо для каждой группы в отдельности).

Поясню это явление на примере симулированных данных. Предположим, у нас имеется некоторая количественная переменная, значения которой разбиты на 3 группы в соответствии с уровнями некоторого фактора. В каждой группе имеется по 100 (случайным образом сгенерированных) нормально распределенных наблюдений. Эти данные приведены ниже на рисунке слева (в виде распределений плотности вероятности). На том же рисунке справа приведено распределение плотности вероятности для всех данных, объединенных без учета их групповой принадлежности. Хорошо видно, что хотя исходные наблюдения в группах А, В и С имели нормальное распределение, после объединения этих наблюдений в одну большую совокупность свойство нормальности исчезает (возникает бимодальное распределение).

Способы проверки нормальности распределения были рассмотрены в одном из предыдущих сообщений, посвященных разведочному анализу данных. Напомню, что такую проверку можно выполнить как визуально, оценив характер распределения значений анализируемой переменной, так и при помощи формальных критериев (таких, например, как критерий Шапиро-Уилка, критерий Колмогорова-Смирнова, критерий Андерсона-Дарлинга и др.).

Визуальная оценка нормальности распределения обычно сводится к изучению формы гистограммы или диаграммы плотности вероятности значений анализируемой переменной, а также графика квантилей. Как отмечено выше, при проверке адекватности модели дисперсионного анализа нормальность распределения значений зависимой переменной должна наблюдаться в каждой экспериментальной группе. При больших объемах наблюдений визуальная оценка нормальности распределения особых затруднений обычно не вызывает. Однако на практике часто приходится иметь дело с небольшим числом наблюдений в каждой группе. Например, в эксперименте с инсектицидами имеется лишь по 12 наблюдений на группу. Попытка использовать гистограммы для проверки условия нормальности распределения в этом случае ни к чему определенному не приведет:

Более информативно выглядят квантильные графики, хотя и с их помощью однозначный вывод о нормальности распределения значений в каждой экспериментальной группе сделать затруднительно:

Как же быть? На помощь приходят свойства нормального распределения. Дело в том, что если значения зависимой переменной в каждой экспериментальной группе распределены нормально, то нормально будут распределены и значения остатков соответствующей линейной модели (см. также здесь). При этом предполагается, что распределение остатков \(\epsilon_i\) имеет среднее значение, равное 0, и некоторое стандартное отклонение \(\sigma_{\epsilon}\). Формально мы можем записать это так: \(\epsilon_i \sim N(0, \sigma_{\epsilon}) \). Таким образом, вместо проверки нормальности распределения значений зависимой переменной в каждой группе, достаточно проверить нормальность распределения остатков модели (число которых, по определению, равно общему объему наблюдений).

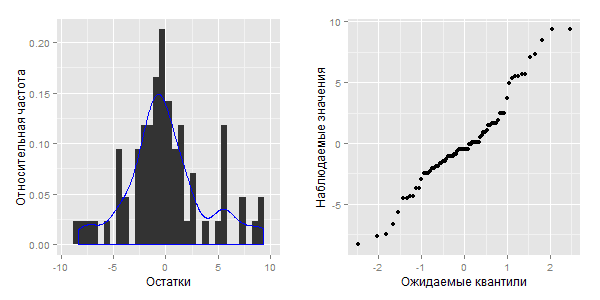
Ниже приведены гистограмма с наложенной кривой плотности вероятности и график квантилей для остатков подогнанной нами ранее модели М:

 

Из приведенных рисунков можно сделать предварительное заключение о том, что распределение остатков модели М не соответствует нормальному (обратите внимание на наличие второго "пика" в правой части гистограммы, а также на S-образную фигуру на графике квантилей). Формально мы можем проверить этот вывод, например, при помощи теста Шапиро-Уилка:

shapiro.test(resid(M))
Shapiro-Wilk normality test
data: resid(M)
W = 0.9601, p-value = 0.02226 

Как видно из полученного Р-значения критерия W (p-value = 0.022),  распределение остатков модели M отличается от нормального. Этот вывод согласуется с визуальной оценкой характера распределения остатков. Таким образом, условие нормальности в отношении модели М не выполняется (что, в общем-то, неудивительно, поскольку мы анализируем результаты подсчета числа выживших насекомых - для описания подобных дискретных количественных переменных следует использовать соответствующее распределение, например, распределение Пуассона). Это значит, что модель М не является адекватной для описания анализируемых данных и, соответственно, мы не можем делать никаких уверенных выводов на ее основе. Ниже будут даны некоторые рекомендации по поводу того, как поступать в таких ситуациях.

Проверка условия однородности групповых дисперсий

Вторым важным условием применимости классического дисперсионного анализа является однородность (также "гомоскедастичность") групповых дисперсий (англ. homogeneity of variance, или homoscedasticity of variance). Речь здесь идет о том, что помимо нормального распределения в каждой группе, значения зависимой переменной должны также иметь одинаковую степень разброса. Необходимость выполнения этого условия определяется способом вычисления внутри- и межгрупповых дисперсий, применяемым в классическом дисперсионном анализе (подробнее см. здесь): при значительно различающихся групповых дисперсиях используемые формулы просто не будут работать корректно.

Способы проверки однородности групповых дисперсий были рассмотрены ранее, и включают как графические, так и формальные методы. Визуальная оценка однородности групповых дисперсий может выполняться по-разному. При большом числе наблюдений в экспериментальных группах это условие можно проверить при помощи диаграмм размахов: сравнение интерквартильных размахов позволяет сделать заключение о том, насколько велики межгрупповые различия в разбросе данных. Для эксперимента с инсектицидами получаем следующую диаграмму (для полноты картины отражены также исходные данные в виде точек):

Из приведенного рисунка хорошо видно, что разброс данных в разных группах неодинаков, что указывает на несоблюдение условия однородности дисперсии.

Подобно тому, как это было сделано нами при проверке условия нормальности, вместо исходных данных мы можем использовать остатки модели и для проверки условия однородности групповых дисперсий. Как и в случае с исходными данными, визуально оценить разброс остатков в каждой группе позволяет диаграмма размахов:

Другим часто используемым способом является изучение графика, на котором по оси Х откладывают предсказанные моделью значения зависимой переменной, а по оси Y - соответствующие остатки. При соблюдении условия однородности дисперсии точки на таком графике не должны формировать каких-либо выраженных паттернов:

Для примера с инсектицидами хорошо видно, что по мере увеличения предсказанных моделью средних групповых значений разброс остатков также увеличивается. Такая "воронкообразная" форма расположения остатков типична для случаев, когда условие однородности групповых дисперсий не выполняется.

Наконец, условие однородности дисперсий можно проверить формально при помощи соответствующих тестов. Одним из наиболее часто используемых является тест Левене (Levene's test). Для рассматриваемых данных получаем:

library(car) # пакет car должен быть предварительно установлен
 
leveneTest(InsectSprays$count, InsectSprays$spray)
Levene's Test for Homogeneity of Variance (center = median)
      Df F value   Pr(>F)   
group  5  3.8214 0.004223 **
      66                    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Неудивительно, что тест Левене также оказался существенно значимым, указывая на выраженную неоднородность групповых дисперсий.

Таким образом, для данных из эксперимента по изучению эффективности инсектицидов не выполняется ни условие нормальности, ни условие однородности групповых дисперсий. Как  следствие, обычный однофакторный дисперсионный анализ не является адекватным методом для этих данных. Как же тогда быть? Возможны разные подходы.


Что делать, когда однофакторный дисперсионный анализ неприменим?

Следует отметить, что однофакторный дисперсионный анализ в определенной степени все же устойчив к нарушениям условий нормальности и гомоскедастичности (Zar 1999). В частности, при одинаковом (или "близком" к одинаковому) числе наблюдений во всех группах метод будет относительно устойчив к нарушениям условия однородности групповых дисперсий. При существенно различающихся объемах наблюдений вероятность ошибки первого рода будет отличаться от уровня значимости \(\alpha\) (обычно 0.05) в степени, пропорциональной неоднородности групповых дисперсий. Если неоднородность возрастает с увеличением числа наблюдений, вероятность ошибки первого рода будет < \(\alpha\) (и наоборот). Дисперсионный анализ устойчив также и к определенным нарушениям условия нормальности, причем чем больше общее число наблюдений, тем выше степень устойчивости.

Какие-либо четкие рекомендации по поводу того, в каких случаях нарушения условий нормальности и гомоскедастичности следует считать допустимыми, очень сложно. Все будет определяться конкретными данными и стоящими перед исследователем задачами. Тем не менее, при серьезных нарушениях этих условий использование параметрического дисперсионного анализа для установления влияния того или иного фактора на изучаемое явление будет некорректным. В зависимости от того, какие именно проблемы возникают при выполнении анализа, решения могут быть разными. Рассмотрим возможные ситуации.

• Распределение в группах нормальное, дисперсии неоднородны: Когда данные в каждой экспериментальной группе распределены нормально, но условие однородности групповых дисперсий не выполняется, можно воспользоваться методом Уэлча (Welch's test). Этот метод позволяет выполнить определенную поправку в числе степеней свободы, что приводит и к соответствующему изменению итогового значения F-критерия. В R однофакторный дисперсионный анализ по Уэлчу выполняется при помощи функции oneway.test(). В качестве альтернативы поправке Уэлча, можно также использовать перестановочные тесты (англ. permutation tests, или randomization tests). Подробно на русском языке эти тесты описаны в книге Шитикова и Розенберга (2013). Одним из пакетов R, позволяющих выполнять перестановочные тесты для линейных моделей, является lmPerm.
• Распределение в группах ненормальное, дисперсии однородны: Когда распределение значений зависимой переменной в экспериментальных группах отличается от нормального, часто помочь может определенная трансформация этих значений. Наиболее обычным способом трансформации количественных переменных является логарифмирование. При работе с относительными частотами и долями часто используется также извлечение квадратного корня из исходных значений. Эти, а также некоторые другие способы, являются частными случаями более общего подхода - степенной трансформации по Боксу-Коксу (англ. Box-Cox transformation). Одним из преимуществ трансформации является также то, что помимо приведения данных к нормальному распределению, она часто позволяет также "стабилизировать" групповые дисперсии (т.е. приводит к выполнению условия гомоскедастичности). Пример того, как это работает, приведен ниже.
  Если при помощи трансформации не удается привести данные к нормальному распределению, вместо классического однофакторного дисперсионного анализа можно применить его непараметрический аналог - ранговый дисперсионный анализ по Краскелу-Уоллису (англ. Kruskal-Wallis one-way analysis of variance by ranks). Этот метод проверяет нулевую гипотезу о равенстве центров (медиан) сравниваемых групп, используя ранги исходных значений, и поэтому особенно хорошо работает при наличии выбросов. Хотя формально метод Краскела-Уоллиса предполагает однородность дисперсий сравниваемых групп, на практике нарушение этого условия имеет малое влияние на конечные результаты (Logan 2010). Поэтому этот метод можно также использовать в ситуациях, когда не выполняются условия как нормальности, так и гомоскедастичности.
• Распределение в группах ненормальное, дисперсии неоднородны: Если трансформация исходных значений зависимой переменной не позволяет привести их к нормальному распределению (в каждой группе) и стабилизировать групповые дисперсии, а также если есть основания полагать, что метод Краскела-Уоллиса не даст надежных результатов (например, из-за существенной неоднородности групповых дисперсий), единственным выходом будет использование статистических моделей, которые не предполагают соблюдение этих условий. Речь идет о классе т.н. обобщенных линейных моделей (англ. Generalized Linear Models). Обобщенные линейные модели - это отдельная огромная тема, к которой я обязательно вернусь в будущем.

В рассмотренном выше примере с инсектицидами мы выяснили, что условия нормальности и гомоскедастичности не выполняются. Для исправления этой ситуации мы можем попробовать трансформировать исходные данные путем логарифмирования и подогнать новую линейную модель на основе трансформированных значений:

M.log <- lm(log(count + 1) ~ spray, data = InsectSprays)
# Обратите внимание: ко всем исходным значениям была добавлена 1.
# Это обычный прием при логарифмировании данных,
# содержащих нулевые значения (поскольку логарифм нуля, как
# известно, не определен).
 
summary(M.log)
 
Call:
lm(formula = log(count + 1) ~ spray, data = InsectSprays)
 
Residuals:
     Min       1Q   Median       3Q      Max 
-0.95261 -0.25946  0.01131  0.25935  1.12683 
 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   2.6967     0.1181  22.829  < 2e-16 ***
sprayB        0.0598     0.1671   0.358    0.721    
sprayC       -1.7441     0.1671 -10.440 1.30e-15 ***
sprayD       -0.9834     0.1671  -5.887 1.45e-07 ***
sprayE       -1.2705     0.1671  -7.605 1.35e-10 ***
sprayF        0.1189     0.1671   0.712    0.479    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
 
Residual standard error: 0.4092 on 66 degrees of freedom
Multiple R-squared:  0.7771, Adjusted R-squared:  0.7602 
F-statistic: 46.01 on 5 and 66 DF,  p-value: < 2.2e-16

Обратите внимание на то, что значение F-критерия, рассчитанное при помощи новой модели (M.log), отличается от исходного (46.01 против исходного 34.7). Хотя в данном случае вывод, который мы делаем в отношении различий инсектицидов по эффективности, не меняется по сравнению с исходным выводом, такая ситуация будет наблюдаться после трансформации данных не всегда.

Тест Шапиро-Уилка показывает, что условие нормальности распределения остатков модели M.log выполняется:

shapiro.test(resid(M.log))
 
 Shapiro-Wilk normality test
 
data:  resid(M.log)
W = 0.9847, p-value = 0.5348

Аналогично, тест Левене показывает, что условие однородности групповых дисперсий теперь также соблюдено:

leveneTest(log(InsectSprays$count + 1), InsectSprays$spray)
Levenes Test for Homogeneity of Variance (center = median)
      Df F value Pr(>F)
group  5  1.8821 0.1093
      66

Таким образом, логарифмирование исходных данных привело к выполнению обоих важных условий применимости однофакторного дисперсионного анализа, и мы можем обоснованно использовать модель M.log для того, чтобы делать заключения по поводу эффективности исследованных инсектицидов.